喇叭摆位是怎么回事？喇叭摆位很重要吗？为何？目标？单靠摆位就能搞定吗？能达到的最好的成果是？

这得先搞懂摆位这件事，喇叭摆位，当然是指移动喇叭在空间中的位置，前后左右；为何喇叭摆在不同位置会有不同的声音？校园广播系统

因为摆在不同位置，离周遭界限面（四面墙、天花板、地板）的距离不同，界限面造成的间接音振幅不同，相对时间（相位）也不同，这些间接音加上直接音的总和，成了我们听见的再生的音乐。

这么说不容易理解，看看图就知道，这张是模拟一个7.8m x 4.35m x 2.6m空间的振幅频率响应，喇叭摆在离背墙2.9m，离侧墙0.7m，聆听位置离背墙1.5m。绿色是界限面全吸音，也就是无响室，是一条直线，音量81dB。

红色则是界限面的吸收率全都是0.2（大约木板的吸收率），结果够惨吧？音量最高可冲到98dB，最低则低于60dB，上下震荡达38dB！而且几乎全都比无响室的81dB高，这是怎么回事？

简单的解说是，不同频率的音波被界限面反射/折射后与另一个音重迭，可能会同相，这就会让音量增加，可能会反相，这就会让音量减低。

这同相/反相，由波长决定，而波长与频率成反比，因此频率也决定相位。六个面造成的交互作用非常复杂，就成了那个惨样...

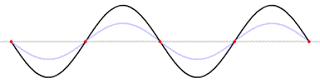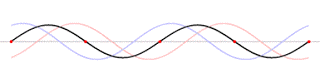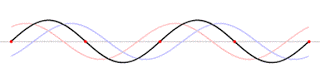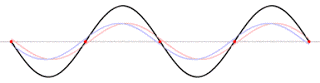
再来慢慢分析看看上面那红色的曲线是怎么回事，先单纯化，设定只有喇叭背墙会反射，其他五个面都全吸收，看起来很规律，为何如此？

音波传到喇叭背墙后，再传到聆听位置，与直接音有时间差，这时间差就成了相位差，相位差0度，就完全加成，相位差180度，就完全抵消，于是就成了这样很 规律的，随着频率倍数变化的图型。看看58Hz处，58Hz的波长5.8m，正是喇叭与背墙距离2.9m的二倍，音波传到喇叭背墙又回到聆听位置，需要比 直接音多走5.8m，正好多了一个波长360度，但反射音会反相，结果成了差180度，与直接音重迭的结果就是直接音被抵消一部分（间接音的振幅）。

再来，加上喇叭退后一半距离（145cm）的对比

同样很规律，而且呈现与290cm的曲线倍数关系，这又是怎么回事？

摆在145cm处，间接音比直接音行程多了290cm，对59Hz而言，等于半波长，180度，再加上反射的反相，就成了360度，等于0度，同相，振幅完全迭加。

摆位造成的效应便是这般波长与距离的魔术，称之为魔术，是因为六个面的间接音加上直接音共七个的交互作用实在太复杂...

再来看看移动多少才能产生足够的效应，红：原先位置，蓝：退后25cm，绿：退后50cm

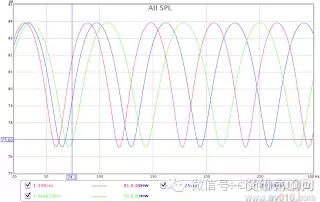
注意看最左边（低频），变化不大，越是右边（高频），变化越大。前面解释过，这高低变化都是因为相位差，而同样的移动量对不同频率而言，相位差不同，波长小的高频，只要移动一点，相位差就很大，波长大的低频，得要移动很多，才能产生足够的相位差，造成够大的变化。校园广播系统

以此例而言，退后50cm，等于改变100cm行程差，对59Hz而言，只有16%，约60度而已；但对177Hz而言，则有50%，180度了～

反过来想，如果177Hz太高或太低，只要移动50cm，效果就很显著；但对59Hz而言，得要移动150cm才能有同样的效应！这几乎不可能做到... 退而求其次，别要求到反相，只要差90度就好，不无小补嘛...那也得要75cm，实在也不算是个小距离...若是31Hz呢？那就得要137cm啰！

然而真正的问题不在此，而在于一移动，并不是只对一个墙面有相对位置改变，而是对四个墙面的相对位置都改变！别忘了，前面这几个推论都是为了容易了解假设 只有喇叭背墙会反射，其他全都是完全吸音，等同于无响室，实际空间当然不是如此。来看看上面那喇叭退后50cm的比较，如果所有界限面的吸收率都是0.2 时，会是这样一团乱吧？177Hz虽然补起来了，但155Hz反倒凹了，70Hz也凸出...真是挖东墙补西墙啊...

一般解决问题的方式是控制变因，偏偏四个墙面变因都连动，无法固定，难...而另一方面，另二个因素，天花板与地板反倒不能动！摆位只能在平面上移动，几 乎无法拉高或降低，若是问题是出在天花板与地板的间接音呢？那真是一翻两瞪眼，没辄！其实还是有点招数，藉由改变喇叭与耳朵的距离，便能改变天花板与地板 间接音的相位（三角函数拿出来算吧...），只是这样又变成六个变因连动了...

还有一点要注意，摆位不只摆喇叭，也摆耳朵，别忘了还有聆听位置背墙。